Il tuo carrello
Non ci sono più articoli nel tuo carrello
- Floriana Giambarresi
- Informazione Tecnica
- 0 commenti
 Recentemente è arrivato sulla mia scrivania un nuovo testo sul cemento armato e sfogliandone l'indice ha catturato la mia attenzione un capitolo in particolare, quello dedicato alla verifica del cemento armato. C'è un bel po' di storia dietro e, nonostante nel momento in cui scrivo le nuove NTC siano ancora ferme (a proposito, davvero dovrebbero essere rilasciate a maggio/giugno?..), di certo ne sono stati fatti di passi in avanti.
Recentemente è arrivato sulla mia scrivania un nuovo testo sul cemento armato e sfogliandone l'indice ha catturato la mia attenzione un capitolo in particolare, quello dedicato alla verifica del cemento armato. C'è un bel po' di storia dietro e, nonostante nel momento in cui scrivo le nuove NTC siano ancora ferme (a proposito, davvero dovrebbero essere rilasciate a maggio/giugno?..), di certo ne sono stati fatti di passi in avanti. Sull'argomento in questione, non tutti sanno che, prima delle Norme tecniche per le costruzioni in vigore, era prassi la verifica delle strutture in cemento armato secondo il metodo delle tensioni ammissibili. Il metodo è ormai stato (quasi) completamente sostituito dal metodo semiprobabilistico agli stati limite. Approfondiamo un po'.
Il metodo delle tensioni ammissibili si basa su un semplice assunto: raggiunta per il materiale una certa tensione (limite, appunto) la struttura cede. In termini matematici, il calcolo si riduce alla verifica della disequazione:
σ < σ ammissibile (3.1)
dove σ rappresenta la massima tensione agente nell’elemento. La tensione ammissibile è calcolata dalla resistenza caratteristica del materiale, ridotta per un coefficiente di sicurezza che tiene conto di diverse incertezze.
Sebbene già dagli anni '90 il più sofisticato metodo agli stati limiti per la verifica del cemento armato sia stato recepito nelle normative nazionali, le tensioni ammissibili hanno fatto da “monopolio” nel mondo dei progettisti fino all’accantonamento imposto dalle Norme tecniche. Inutile dirlo, il successo era dovuto, sì all’inerzia dei progettisti nel cambiare metodo, ma anche e soprattutto alla facilità di utilizzo. Perché quindi imporre a livello normativo una deviazione di rotta? La risposta a questa domanda si basa su un secondo semplice assunto: quando il materiale raggiunge la resistenza massima… non succede nulla!
Materiali come il calcestruzzo e (soprattutto) l’acciaio non sono materiali fragili. Ciò significa che, anche quando viene raggiunto il limite massimo di resistenza, sono in grado di deformarsi ulteriormente conservando rigidezza. Visto da ulteriore punto di vista: la deformazione che porta a rottura il materiale non è uguale alla deformazione al limite massimo di resistenza. In figura 3.1 è rappresentato il diagramma sforzo-deformazione tipico dell’acciaio. Notate come l’effettiva rottura del materiale si verifichi molto dopo il valore εe in cui il materiale risponde con il limite massimo di resistenza.
Non è del tutto vero dire che superato il limite “non succede nulla”. È più esatto dire che possono succedere molte cose, ma non necessariamente il collasso strutturale.
Ritorniamo sulla figura 3.1. Il diagramma è ricavato da un provino sottoposto a trazione sino a rottura. La trazione massima registrata è effettivamente un limite di rottura: non è in grado di resistere a trazioni maggiori perché si avrebbero tensioni superiori al limite massimo che il materiale è in grado di mobilitare.
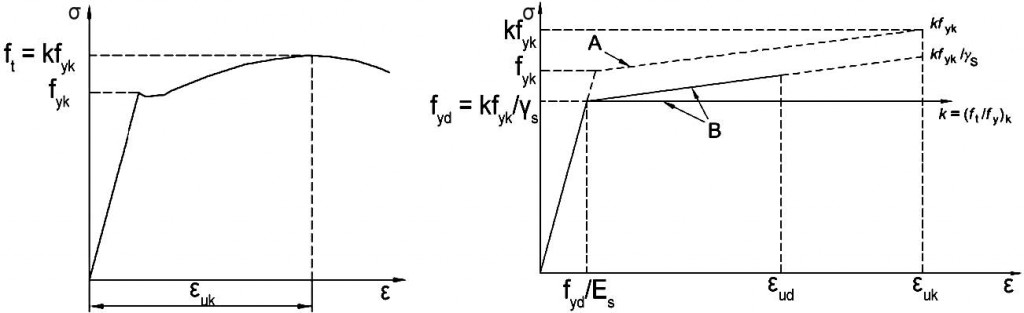
- Figura 3.1. Tipico diagramma sforzo-deformazione acciaio- reale a sinistra, idealizzato a destra
Per il provino sottoposto a trazione il raggiungimento del limite di rottura del materiale coincide con il raggiungimento del limite di resistenza della sezione.
Ora consideriamo la trave inflessa di figura 3.2. La sezione maggiormente sollecitata è soggetta ad un momento flettente M = M₁. Ipotizzate che il momento provochi il raggiungimento (nel lembo superiore ed inferiore) della tensione massima del materiale σ = σmax.

- Figura 3.2. Trave inflesse al limite di resistenza e oltre…
Aumentiamo ora (di poco) il momento flettente. In accordo con il metodo delle tensioni ammissibili, la trave dovrebbe cedere: stiamo andando oltre i limiti. È vero che nei due lembi la tensione non può aumentare; è, però, altrettanto vero che è in grado di sopportare ulteriori deformazioni: la deformazione al limite di rottura è maggiore della deformazione al limite di resistenza ε > εe (vedi il diagramma). Aumentando il momento, si generano nella sezione gli sforzi rappresentati in figura 3.2, contrastando il momento applicato con un momento reagente M2 maggiore di M1.
Riassumendo: il momento limite MRd che porta alla rottura la sezione è maggiore del momento M0 che produce nella zona più sollecitata la tensione limite del materiale. Non sappiamo ancora quando la sezione si romperà e spenderemo gran parte del testo nel trattare metodi che ci permetteranno di prevedere i limiti di resistenza delle sezioni.
Ora però sappiamo perché il metodo agli stati limite è più sofisticato ed è stato preferito in sede normativa (nazionale ed europea soprattutto).
Il metodo agli stati limite
Passando da tensioni limite a stati limite, la semplice e intuitiva verifica rappresentata dalla (3.1) prende una forma molto più generica (e un po’ insapore):Ed ≤ Rd (3.2)
dove Ed rappresenta la sollecitazione agente di progetto ed Rd la sollecitazione resistente di progetto. A seconda dei casi Ed può essere un’azione di taglio, un momento flettente, una torsione, ma anche un’azione concentrata su una platea ecc. Rd è l’equivalente di Ed, ma di intensità tale da portare l’elemento (o la struttura) in uno stato limite. La difficoltà, ma anche l’opportunità, è quella di poter considerare la struttura sino al suo reale limite, caratterizzato da un complesso (più o meno) stato di sollecitazione/deformazione interno.
Con questo abbiamo inquadrato il concetto di stato limite. Ora approfondiamo il perché della definizione di semiprobabilistico del metodo. Descrivendo la (3.2) abbiamo parlato di sollecitazioni di progetto e resistenze di progetto. Le definizioni, apparentemente intuitive, sono in realtà qualcosa di più complesso. È nel “di progetto” che si nasconde l’impronta “probabilistica” del normatore. Il “di progetto” si deve leggere: che ha probabilità X di essere superata (la sollecitazione), o di non essere raggiunta (la resistenza), durante la vita utile della struttura.
Dato che le sollecitazioni sono provocate dalle azioni e le resistenze dipendono dai materiali, la normativa agisce su di esse per determinare la “probabilità X”.
Azioni caratteristiche, di progetto e combinazioni di carico
La norma parte dalla definizione di valore caratteristico di una azione. La definizione data al punto 2.5.2 è: “Si definisce valore caratteristico Qk di un’azione variabile il valore corrispondente ad un frattile pari al 95% della popolazione dei massimi, in relazione al periodo di riferimento dell’azione variabile stessa”.Semplifichiamola con un esempio. Vogliamo calcolare il valore caratteristico delle azioni variabili sul solaio di una casa; la casa deve durare 50 anni (il periodo di riferimento, appunto).
Prendo 100 case uguali, monitoro il carico agente sui solai di tutte le case per 50 anni. Alla fine dei 50 anni avrò calcolato un massimo per ogni casa. Ordino i massimi in modo crescente: il 95esimo massimo è il valore caratteristico del carico variabile. Detto altrimenti, quello che è stato superato solo il 5% dei casi.
Noti i valori caratteristici delle azioni, i valori di progetto sono ottenuti con il metodo dei coefficienti parziali di sicurezza. Il valore di progetto dell’azione F è calcolato partendo dal valore caratteristico nel seguente modo:
Fd = γk · Fk
Il coefficiente γk è (appunto) il coefficiente parziale di sicurezza dell’azione Fk. Attraverso i coefficienti parziali la normativa raggiunge il valore statistico di probabilità di non superamento che il legislatore ritiene opportuno.
L’argomento deve essere completato parlando delle combinazioni fra azioni. Tutte le strutture possono essere soggette a differenti azioni: vento, neve, sisma sono le più classiche. È improbabile che tutte possano agire con la massima intensità: la nevicata “del secolo” non verrà nello stesso giorno della “bufera del secolo”. Al contrario, c’è una possibilità non trascurabile che, durante il periodo in cui la casa è sommersa dalla nevicata del secolo, vengano giornate ventose. Tutte e due le azioni possono verificarsi
contemporaneamente, ma non tutte con i valori massimi di progetto.
Questa considerazione banale è alla base della definizione dei coefficienti di combinazione ψ. La normativa definisce tre tipologie di coefficienti di combinazione: ψ0, ψ1,ψ2.
In particolare (NTC – 2.5.2):
• ψ2 Fk, valore quasi permanente: la media della distribuzione temporale dell’intensità
• ψ1 Fk, valore frequente: il valore corrispondente al frattile del 95% della distribuzione temporale dell’intensità e cioè che è superato per una limitata frazione del periodo di riferimento
• ψ0 Fk, valore raro: il valore della durata breve ma ancora significativa nei riguardi della possibile concomitanza con altre azioni variabili.
L’argomento è più semplice di quanto non risulti leggendo la norma. I coefficienti di combinazione non “lavorano” per regolare la probabilità di superamento di una certa azione; riportano il carico al valore che è probabile registrare in un determinato periodo.
Riprendendo l’osservazione delle “100 case nei 50 anni”, il valore del carico che ha sollecitato mediamente il solaio per 25 anni è dato da ψ2 Fk. Quello che ha sollecitato i solai per 5% · 50 anni = 2.5 anni è dato da ψ1 Fk. Genericamente, ancora meno frequente è il valore del carico raro (la norma non dà indicazione numerica sulla probabilità di non superamento). Alcuni valori dei coefficienti di combinazione previsti dalla normativa sono riportati nella seguente tabella.
Tabella: Coefficienti di combinazione secondo le NTC
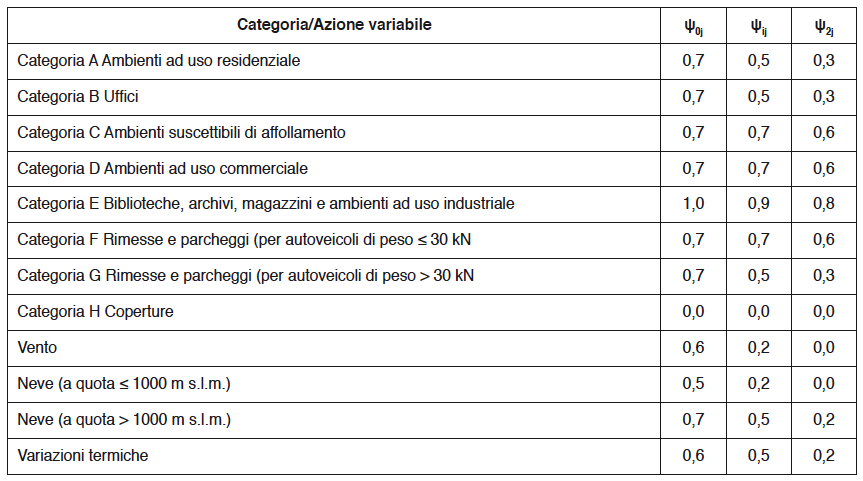
- Coefficienti di combinazione secondo NTC
dove
G1 sono le azioni permanenti strutturali (pesi propri delle strutture)
G2 sono le azioni permanenti non-strutturali (massetti, partizioni, ecc.)
P sono le azioni di precompressione
Q sono le azioni variabili.
Da notare: per le azioni permanenti i coefficienti di combinazione non hanno significato fisico (o meglio, sono sempre pari a 1). Tra le azioni variabili, una è intesa come principale, e quindi presa con il suo valore massimo di progetto γQ1 · Qk1. Le altre sono combinate attraverso i coefficienti di combinazione. Questo influisce non poco nella definizione delle combinazioni di progetto; a turno andrebbero considerate come principali tutte le azioni variabili. È giusto osservare che, spesso, è noto a priori quali siano le azioni più
gravose per la struttura; solo queste possono essere considerate come fondamentali.
Brevemente, lo approfondiamo nel libro sulle sezioni in cemento armato, sono due i principali stati limite considerati nell’analisi: gli stati limite ultimi (SLU) e gli stati limite di esercizio (SLE).
Le verifiche richieste allo stato limite ultimo servono per accertare che la struttura non possa cedere rovinosamente causando danni a cose e persone. Le verifiche allo stato limite di esercizio si fanno per accertarsi che la struttura rimanga funzionale durante la vita utile prevista per la struttura. Un cedimento o una deformazione eccessiva non provocano il crollo di una struttura, ma possono inficiarne l’estetica o la funzionalità, ad esempio interferendo con elementi non strutturali. La “classica” verifica allo stato limite di esercizio è quella a fessurazione del calcestruzzo.
In funzione delle verifiche che si intendono effettuare, la norma definisce diverse combinazioni di carico:

Materiali: valori caratteristici e valori di progetto
La definizione dei parametri meccanici che caratterizzano i materiali segue la stessa filosofia applicata per le azioni. La resistenza di calcolo si basa sempre sul valore caratteristico fk, inteso come il valore con probabilità X di essere superato (solitamente il 95%).La resistenza di calcolo è, quindi, calcolata come:
fd = fk/γM
Per il calcestruzzo le resistenze di calcolo sono così date:
fcd = αcc fck/γC
dove
fck è la resistenza cilindrica del calcestruzzo
γC = 1.5
αcc = 0.85, è il coefficiente che tiene conto di riduzioni di resistenza per carichi di lunga durata.
È bene osservare che la resistenza a compressione è calcolata in laboratorio in due modi: su provini di forma cubica e su provini di forma cilindrica. I due valori di resistenza sono collegati ma non identici. In questo senso fck è definita come resistenza cilindrica.
A trazione vale la relazione:
ftd = ftk/γC
con ovvio significato dei termini.
Per l’acciaio d’armatura vale:
fyd = fyk/γs
dove
γs = 1.15
fyk è la resistenza di snervamento dell’acciaio.
Hai altro da aggiungere?
Per approfondire
Bibliografia:
Sezioni in cemento armato 2.0: soluzioni semplici per problemi complessi
di Marco Cavalieri, Studio CCProgetti

Commenti (0)
Aggiungi nuovo commento