Quale fattore di sicurezza adottare nelle analisi di stabilità globale?

Le normative tecniche nazionali che si sono succedute negli ultimi decenni sono sempre state molto chiare sui metodi di adozione del più appropriato fattore di sicurezzarelativo alle analisi di stabilità globali, che essi siano afferenti un versante integro, una frana da consolidare oppure un’opera di sostengo; eppure, sono ancora molti gli enti che contestano fattori di sicurezza inferiori ad 1.3, così come sono ancora molti i tecnici che ritengono (scrivendolo nelle proprie relazioni geologiche e geotecniche) debba essere rispettata la condizione:

Fs ≥ 1.3

ignorando che la stessa ha la medesima valenza di una leggenda metropolitana.

A tal proposito il “vecchio” DM 11.03.1988 prescriveva:

• Muri di sostengo: il coefficiente di sicurezza non deve risultare inferiore a 1,3 (par. D.4.5)
• Paratie: i valori dei coefficienti di sicurezza saranno assunti dal progettista e giustificati sulla base del grado di affidabilità dei dati disponibili e del modello di calcolo adottato (par. D.7.2)
• Pendii: il valore del coefficiente di sicurezza sarà assunto dal progettista e giustificato sulla base delle considerazioni relative ….. (par. G.2.3)
• Fronti di scavo: nel caso di terreni omogenei e nei quali le pressioni neutre siano note con sufficiente attendibilità, il coefficiente di sicurezza non deve essere minore di 1,3 (par. G.3.1)

Allo stesso modo l’attuale DM 14.01.2008 prescrive:

• Muri di sostengo: la norma non è sufficientemente chiara sull’argomento, tanto che la successiva Circolare esplicativa 617/2009 (par. C6.5.3.1.1) rimanda alla sezione dedicata alle opere di materiali sciolti e ai fronti di scavo, laddove si legge che “I livelli di sicurezza prescelti devono essere giustificati in relazione alle conseguenze di raggiungimento dello stato limite ultimo” (par. 6.8.3)
• Paratie: valgono le medesime considerazioni del caso precedente
• Pendii: il grado di sicurezza ritenuto accettabile dal progettista deve essere giustificato sulla base del livello di conoscenze raggiunto ….. (par. 6.3.4)
• Fronti di scavo: valgono le medesime considerazioni dei muri e delle paratie
  
  

Evitando inutili commenti, dal momento che le norme sono sufficientemente chiare sull’argomento, si vede facilmente che il problema è tutto incentrato nella giustificazione del grado di sicurezza che si vuole raggiungere in sede progettuale per la quale s’impone il ricorso alla seguente equazione:

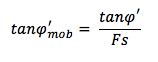
In essa vi compaiono:

f’: = angolo di resistenza al taglio di progetto, il cui valore discende dai coefficienti parziali previsti dall’Approccio normativo considerato
Fs = fattore di sicurezza
f’_mob = angolo di resistenza al taglio mobilitato.

La validità di tale equazione deriva dal fatto che Fs esprime il rapporto tra la resistenza disponibile (che può espressa in termini di forze o momenti) e lo sforzo (o il momento) di taglio destabilizzante che agisce lungo una determinata superficie di scivolamento, per i cui dettagli si rimanda ai miei due testi Introduzione alla Meccanica delle Terre e a Manuale avanzato di Meccanica delle Terre.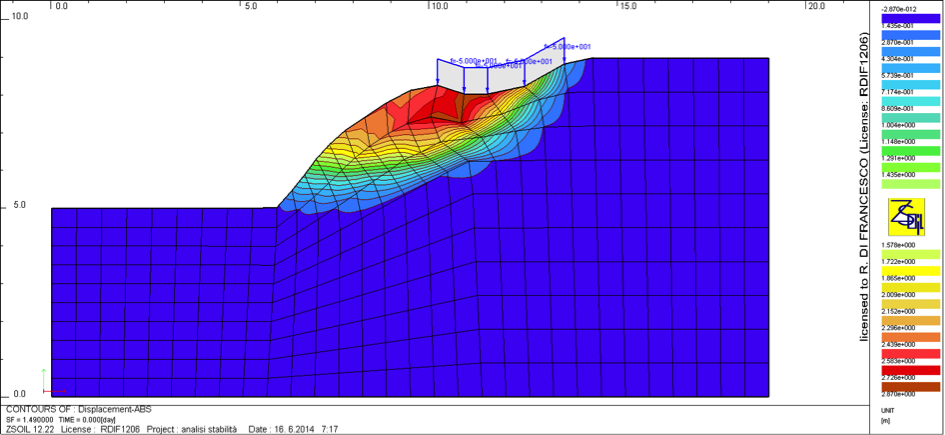


Nel caso del modello ad elementi finiti relativo alla figura in alto, per un angolo di resistenza al taglio di 30° (immutato secondo l’Approccio 2, essendo unitario il coefficiente parziale di tabella 6.2.II – colonna M1 delle NTC) ed un carico uniformemente distribuito q = 50 kN/ml, è stato ottenuto un coefficiente di sicurezza Fs = 1.49 che fornisce un angolo di resistenza al taglio mobilitato di:

tan^-1 (tanf’/FS) =  f’_mob: 21.2°

Tale risultato implica che esiste una resistenza disponibile pari a:

  f’_disp: 30° - 21.1° = 8.8°

Rapportando la resistenza disponibile a quella iniziale si ottiene:

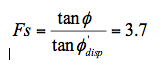
che assume il ruolo di moltiplicatore dei carichi necessario per raggiungere la condizione di potenziale collasso corrispondente a Fs = 1.

Al fine di verificare l’attendibilità del metodo sono stati progressivamente incrementati i carichi nel modello ad elementi finiti iniziale e sono stati ottenuti i seguenti risultati:

• q =    50 kN/ml;          Fs = 1.49
• q₁ = 100 kN/ml;          Fs = 1.19
• q₂ = 150 kN/ml;          Fs = 1.03
• q₃ = 160 kN/ml;          Fs = 1.01
• q₃ = 165 kN/ml;          Fs = 1
  
  

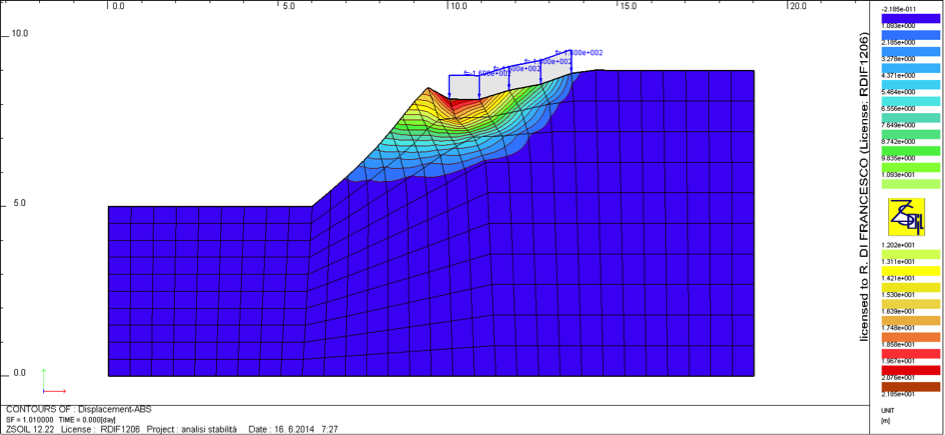
In pratica, il collasso nel modello ad elementi finiti è avvenuto per la condizione:

q_lim = 165 kN/ml = 3.3q

molto vicina al valore teorico di 3.7 relativo invece ad un modello classico basato sulle leggi rigido-plastiche: un risultato che implica che per passare dal coefficiente di sicurezza iniziale al collasso occorre incrementare di 3.3 volte i carichi di progetto!

Continuando con gli esempi, nel caso di un angolo di resistenza al taglio di 30° e di un fattore di sicurezza di 1.25 si ottiene:

• f’_mob: 24.8°
• f’_disp:    5.2°
•  f’/f’_disp: 5.8

Il risultato implica, dal momento che i modelli di analisi sono non lineari, che il fattore di carico non è 1.25 (identificativo del fattore di sicurezza) ma 5.8, denotando un’elevata riserva di resistenza che deve essere esplicitata nelle relazioni specialistiche per giustificare il coefficiente di sicurezza adottato (in questo caso Fs =  1.25) nei confronti degli enti che lo richiedono (Geni Civili).

Rimane un’ultima domanda da porsi: da dove trae origine l’equazione proposta?
Dal buon vecchio Bromhead (1991, Stabilità dei pendii, Dario Flaccovio Editore) che, anche se scritto con un linguaggio superato, rimane ancora un valido testo di riferimento.
 

Romolo Di Francesco